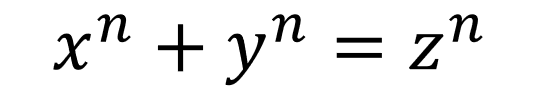フェルマーの最終定理
聞いたことくらいはあるでしょうか?
皆さん嫌いな数学のお話です。。。
ただもうちょっとだけ待ってください!
せっかくこの記事を見てくれたのならせめて
フェルマーの最終定理っていうのが
何なのか?
ということだけでもわかってもらいたいので><
【フェルマーの最終定理】
nが3以上の整数の時に、この式を満たす正(プラス)の整数x,y,zがない
これだけ
このとってもシンプルな1つの問題がフェルマーの最終定理だ
xとかyとかzの右上にのっかってるやつは指数ってやつ、◯乗とかいうやつ
たとえば32=3×3=9 といったかんじ
もうちょっと記憶を呼び起こしてほしい
x2+y2=z2
こんな式を覚えてないだろうか?
これならどうだ!!!

そう、三平方の定理ってやつ
こっからルート√とかいうのもでてきたなーなんてなつかしんでもらったところで
フェルマーの最終定理に戻ろう
フェルマーの最終定理のn=2のときが
三平方の定理
でn=2のときなら
32+42=9+16=25=52
ということで
32+42=52
がなりたっている
ほかにも成り立つx,y,zの組み合わせは色々ある
つまりn=2のときはなりたつのだ
だからフェルマーの最終定理にはnが3以上の整数の時にという条件がつく
n=2は成り立つけど、nが3以上だと成り立たないというのがフェルマーの最終定理の意味するところ
さて、これをきいてどう思っただろうか?
意外か、そうでもないか?
(そもそもだからなんだ?かもしれないが…)
でもやっぱり数字って無限にあるんだし
「nが2でもなりたつならnもxもyもzも何でもいいっていう条件なら成り立ちそう」
と自分は思った
でも成り立たないわけである 不思議だ~
そしてここからがフェルマーの最終定理を面白くしているポイント
このフェルマーの最終定理は17世紀にフェルマーによって予想された
ここで予想といっているのはフェルマーが証明をのこしてくれなかったからである
数学においては証明されてはじめて予想が定理になる
ただこの一文を残した
『私はこの命題の真に驚くべき証明をもっているが、余白が狭すぎるのでここに記すことはできない』
なめてんのかーーーーーー!!
そして驚くことはもう一つ
この予想の証明に数々の超絶天才数学者達が挑んだにも関わらず
350年以上かかったのだ
※まぐろの寿命は平均20年
350年の時を経て、ワイルズという数学者によって1995年に証明された
この作品はそんな、「数多の天才数学者とフェルマーの最終定理を巡る戦い」の物語
数学や科学が好き、興味がある
伝記が好き
ノンフィクションのワクワクする本が読みたい
数学の歴史を知りたい
フェルマーの最終定理は一人の天才のある瞬間のひらめきで証明されたというものではない
数多の数学者が挑戦し敗れながらも
切り開いてきた新たな道
少しずつ糸口を探していった積み重ねがあって
はじめてなしとげられた
フェルマーの最終定理の証明の歴史を追うことは
数学の歴史を追うことにもなる
数学の歴史
数学とはどのような学問なのか
数学者がなぜ数学に取り組むのか
そんなことが青春小説のように楽しめながら知れてしまう
とってもお得な作品
数学の知識があったほうが読みやすいのは確かだが
なくても読めるように工夫されている
この記事ではいきなり読むよりはちょっとでも
読みやすくするためにポイントとなった点を紹介する
フェルマーの最終定理と数学の歴史
フェルマーの最終定理をめぐる物語は、数学の歴史と分かち難くからみ合い、数論の主要なテーマはすべてこれにかかわっている。
この物語は、数学を全身させるものは何かという問題、そして、数学者を奮い立たせる者は何かという、おそらくはいっそう重要な問題に対して比類のない洞察を与えてくれる。数学界の偉大な英雄たちを一人残らず巻き込んで展開する、勇気、不正、ずるさ、そして悲しみに彩られた魅力あふれる冒険物語ーその中心にあるのが、フェルマーの最終定理なのである。
先程もふれたようにフェルマーの最終定理は一人の天才だけの力によって証明されたというものではない
ガロア、オイラー、ガウスといった天才達も取り組んだ
この人達も神武以来の天才だから覚えておいておくとGood
彼ら単体の歴史もこの本に書いてあってそれぞれおもしろい
そしてその取り組む過程で、フェルマーの最終定理の証明には至らずとも多くの発見をし数学の新しい分野を切り開いてきた
そうして切り開いてきたすべての知恵を集結させて証明されたのがフェルマーの最終定理
この本ではフェルマーの最終定理を追いながら歴史が追いやすいように工夫されていて
古くはギリシャ時代のユークリッドやピタゴラスまで触れてくれる
最初に紹介した三平方の定理はピタゴラスが見つけたので
ピタゴラスの定理と呼ばれる方が世界的にはスタンダート
ユークリッドは数学の基礎をつくったと言われる人たち
ガロア、オイラー、ガウス、ユークリッド、ピタゴラスっていうすっげーやつの話がでてくる
数学の完全性
クルト・ゲーデルは、数学は論理的に完全ではありえないことを数学者たちに認めさせたのだ。しかもゲーデルの研究は、フェルマーの最終定理のような問題は解けないかもしれないということを暗にほのめかしていたのである。
これはちょっとむずかしい話で自分も説明できないのだが
数学って「ある少数の公理をもとに積み重ねていて、どこまでも整然としていて厳密なもの」だと思ってた
当時の数学者もそう思っていた
ただ、そうではないということを証明してしまったというのだ
これもなんというかすっごく奥深い
数学において
証明できないと証明することも1つの証明なのだ
たぶんこの証明に数字はほとんどでてこにない
本来数学ってのは数の学問ではない
数学を表す英語(mathmatics)の語源といわれているギリシャ語の「マテーマタ(mathemata)」は「学ぶべき事」という意味
数学の完全性を示そうと取り組んだ数学者達
そして数学の完全性が成り立たないことを証明してしまった数学者
そこらへんの「数学というのはどういう学問なのか」
を問うための取り組みの部分も非常に興味深い
そして引用に示したように
このことから「フェルマーの最終定理が証明できないかもしれない」
ということがフェルマーの最終定理をより強大な敵としていった
数学ってのはなんだか奥深く神秘的らしい
学問の発展の法則
一見すると関係のなさそうなテーマ同士が結びつくことは、どんな学問分野においてもそうであるように、数学においても建設的な意義をもっている。というのも、そんな結びつきが存在することは、両方のテーマをいっそう豊かにする基本的心理の存在をほのめかすからである。
一見関係ない、あるいは矛盾するものが、両方を内包するような高次の考えとして1つの理論を生み出すことがある
ここらへんの話は弁証法っていうのを学んだりするとでてくるんだけど
ちょっと自分もここも理解はあまいので、興味ある方は調べてみてほしい
物理も一見関係ない、あるいは矛盾するものを折り超えるために高次な法則がうまれていった
同じように数学でも起こる
フェルマーの最終定理を証明するためには
「モジュラー形式と楕円方程式というものが実質的には同じ」という予想を証明する必要があった
その予想の名前は「谷山=志村予想」と呼ばれる
そう!日本人が導いた予想なのである
さて、これまた最初にも言ったが数学では証明しないと定理にならない
だからといって予想に価値がないかというとそんなことはない
なんてたって「フェルマーの最終予想」という一つの問題提起があったからこそ発展した数学の分野は計り知れない
楕円方程式とモジュラー形式、これまら自分も全然知らないが
両者に関係性があるなどとは誰も思っていなかったらしい
「正しい問題設定をする」というのは時に、問題を解くことそのものよりも難しく重要である
これは数学に限らず、あらゆる学問、ひいてはビジネスや人生でも使える考え方である
ということで、フェルマーの最終定理の証明には日本人数学者もおおいに貢献したということも是非知っておいてほしい
そして、一見関係なさそうなもの、矛盾しているものを、まとめ上げた時、そこには果てしない可能性が広がっていることもよく心にとめておきたい
・「正しい問題設定」は大切
・一見関係なさそうなもの、矛盾しているものを、まとめ上げた時、そこには果てしない可能性が広がっている
・フェルマーの最終定理の証明には日本人数学者である谷山さん、志村さんが大いに貢献した
『フェルマーの最終定理』まとめ
- フェルマーの最終定理に天才たちが取り組む過程で多くの新たな数学がうまれた。その歴史も学べる。
- 数学の神秘性や奥深さを知れる。
- フェルマーの最終定理の歴史には科学の発展のエッセンスも詰まっている。
- フェルマーの最終定理の証明には日本人数学者も大きく貢献した。
文庫で450pとボリュームは多いが、この本1冊から得ることができる学びはあまりにも多いです。
しかもワクワクしながら読めるように配慮されていて読みやすいです。
そもそもこの本をオススメしてくれたのも文系の人だったので、数学が苦手な人でも楽しむことはできるはずです。
是非、手にとって数学の奥深さや神秘さを味わいつつ、小説のような、あるいはそれ以上にワクワクできる発見物語を味わってみてください!
また、この本よりももっと読みやすい導入に使える本として『数学ガール』という本もあるので興味がある方はそちらもご覧になってみてください。
ここまで読んで頂きありがとうございました。